What is a Segment Tree?

A Segment Tree is a tree-based data structure used to efficiently handle range-based queries on an array. It allows us to query information (such as sum, minimum, or maximum) over a subarray and also update elements efficiently.

In simple terms, a Segment Tree is used when:

You need to answer range queries frequently
The array values can change over time

Why do we need a Segment Tree?

Consider an array: arr = [a₁, a₂, a₃, a₄, …, aₙ]

Suppose we have two types of queries:

Range Query: Find the sum of elements from index l to r
Update Query: Update the value at a specific index

Problem with Prefix Sum

Using a prefix sum array, we can answer range sum queries in O(1) time. However, when an update happens:

The array value changes
The prefix sum array must be rebuilt
This rebuild takes O(n) time

If there are many update queries, the total time complexity becomesO(q · n), which is not feasible for large inputs (e.g., n = 10⁶).

This leads to TLE (Time Limit Exceeded).

How Segment Tree Solves This

A Segment Tree solves this problem efficiently by:

Answering range queries in O(log n)
Handling updates in O(log n)

So, even if we have many queries:

Total time complexity becomes O(q log n)
This is efficient and feasible for large inputs

Conclusion

Prefix sums fail when frequent updates are involved
Segment Trees handle both queries and updates efficiently
It is a reliable and scalable solution for range-based problems

That is why Segment Trees are widely used in competitive programming and high-performance systems.

Structure of the Segment Tree

We can take a divide-and-conquer approach when it comes to array segments. We compute and store the sum of the elements of the whole array, i.e., the sum of the segment a[0 … n - 1]

We then split the array into two halves a[0 … (n - 1)/2] and a[(n + 1)/2 … n - 1] and compute the sum of each half and store them. Each of these two halves is again split into two smaller halves, and this process continues until all segments reach size 1.

These segments can be viewed as forming a binary tree. The root of this tree represents the segment
a[0 … n - 1], and each internal node has exactly two children. This is why the data structure is called a Segment Tree, even though in most implementations the tree is not constructed explicitly.

Below is a visual representation of a Segment Tree built over the array: a = [1, 3, -2, 8, -7]

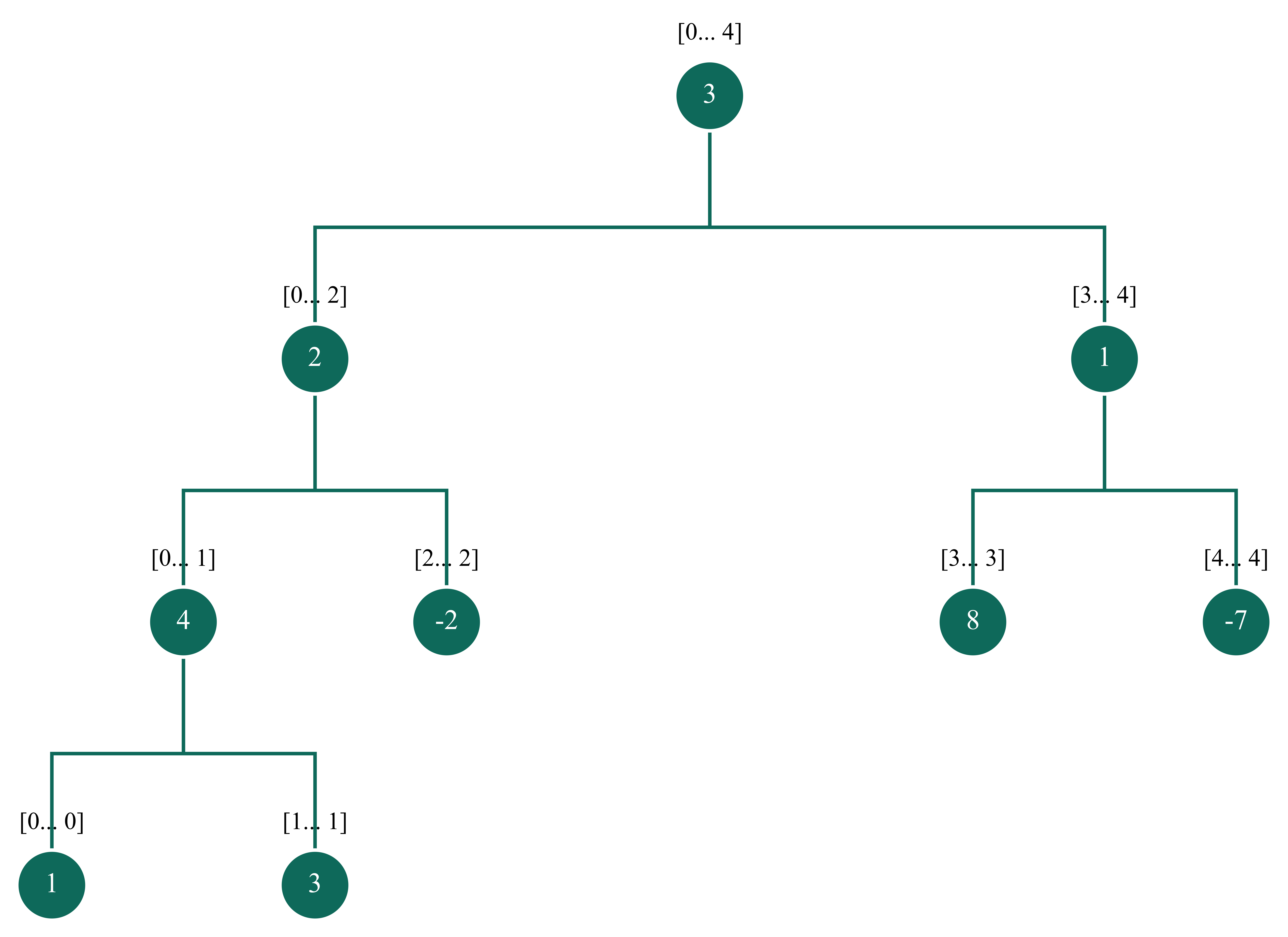
The height of a Segment Tree is O(log n), because when moving from the root to the leaves, the size of the segment is reduced by approximately half at each level.

Construction of the Segment Tree

Before constructing a Segment Tree, we need to decide two important things:

The value stored at each node — for example, in a sum Segment Tree, each node stores the sum of elements in its range[l, r].
The merge operation — this defines how the values of two child nodes are combined. In a sum Segment Tree, the values are merged by adding them.

A node is called a leaf node if its segment represents only a single element of the array. In that case, the value stored in the node is simply the corresponding array element.

To build the Segment Tree, we start from the leaf nodes and assign their values. Using the merge operation, we then compute the values of their parent nodes. This process continues until we reach the root node, which represents the entire array.

In practice, the construction is described recursively in the opposite direction, starting from the root node:

Recursively construct the left child node
Recursively construct the right child node
Merge the values of both children to compute the current node

By starting this process from the root node, we are able to construct the complete Segment Tree.

The time complexity of building a Segment Tree is O(n), assuming the merge operation takes constant time, since each node is processed exactly once.

Sum Queries and Update Queries

Sum Queries

To compute the sum of a range [l, r], we traverse the Segment Tree and use the precomputed sums stored in the nodes.

If the current node exactly matches the query range, return its stored sum.
If the query lies fully in one child, recursively move to that child.
If the query overlaps both children, split it, compute both parts, and add the results.

Since only a limited number of nodes are visited at each level and the height of the tree is O(log n), the total time complexity is O(log n).

Update Queries

An update query modifies a single element in the array. We recursively traverse the tree to the leaf node representing that index and update its value.

While returning back up the tree, we recompute the values of all affected parent nodes using the merge operation.

Since only one node per level is updated, the time complexity of an update query is also O(log n).

Implementation

There are may ways to implement a Segment Tree. One common approach is to use an array-based representation, where the tree is stored in a flat array. This method is efficient in terms of both time and space. if want to know why we use array to represent segment tree please refer to the CP-Algorithms.

Array-Based Representation

In an array-based representation, the Segment Tree is stored in an array of size 4 * n to accommodate all nodes. The root node is at index 0, and for any node at index i:

The left child is at index 2 * i + 1
The right child is at index 2 * i + 2

This Array-Based Representation allows for efficient traversal and updates without the need for explicit pointers.

📌 Variable Notation

idx → index of the current node in the segment tree array
l → left boundary of the segment represented by the current node
r → right boundary of the segment represented by the current node
ql → left boundary of the query update
qr → right boundary of the query update
pos → index of the element for a point update
val → value to be added during a point update

Build Function

The build function constructs the segment tree using a recursive divide-and-conquer strategy. It takes the current segment tree index idx, the array range [l, r], and the input array arr.

When l == r, the recursion reaches a leaf node, representing a single element of the array. At this point, the value arr[l] is directly stored in seg[idx].

Otherwise, the current range is split at mid into two subranges:[l, mid] and [mid + 1, r]. The function then recursively builds the left child at 2 * idx + 1 and the right child at 2 * idx + 2.

After both children are constructed, the current node aggregates their values. In this implementation, the aggregation operation is sum:seg[idx] = seg[2 * idx + 1] + seg[2 * idx + 2]. This process continues upward until the root node is built.

Range Sum Query Function

The rangeSumQuery function is used to compute the sum of elements within a given query range [ql, qr] using the segment tree. It operates on a node at index idx representing the segment [l, r].

To answer a query efficiently, the algorithm evaluates three possible overlap cases between the current segment and the query range.

No Overlap: If the segment [l, r] lies completely outside the query range [ql, qr], the function returns 0, since it contributes nothing to the sum.
Complete Overlap: If the segment [l, r] is fully contained within the query range [ql, qr], the precomputed value seg[idx] is returned directly. This avoids unnecessary recursion.
Partial Overlap: If the segment is partially inside and partially outside the query range, the segment is divided at mid into two halves:[l, mid] and [mid + 1, r]. The query is executed recursively on both children, and the final result is the sum of the left and right subqueries.

This operation is read-only. The segment tree is not modified during a range sum query, as no updates are required. The result is obtained purely through traversal and aggregation.

Point Update Function

The pointUpdate operation updates the value at a specific array index and reflects this change in the segment tree. It takes five parameters: the target index, the new value val, the segment tree index idx, and the segment range [l, r].

The update process follows a binary-search–like traversal. At each recursive step, the current segment [l, r] is divided at mid to determine whether the target index lies in the left subtree [l, mid] or the right subtree [mid + 1, r].

This process continues recursively until l === r, which represents a leaf node. This node corresponds exactly to the update index, and its value is increased by val.

While returning from recursion, each ancestor node is recomputed to maintain correctness of the tree. For a sum segment tree, the parent value is updated as:
seg[idx] = seg[2 * idx + 1] + seg[2 * idx + 2]
This ensures that all affected ranges reflect the updated index.

Complete Segment Tree Code

Here is a sample code snippet for Segment Tree sum operations:

Summary

I have explained Segment Trees based on my own understanding and what I learned while studying them. I hope this guide is helpful to you. If you notice any mistakes or areas for improvement, please feel free to report them.

Practice Problem

You can practice Segment Tree problems on various competitive programming platforms. Here are a few recommended problems to get you started:

These problems will help you understand the implementation and application of Segment Trees in various scenarios. Happy coding!